Graph differential equations
The quadratic will be zero at the two points x 2 pm 2sqrt 2. The graph above shows the predator population in blue and the prey population in red and is generated when.

Linear Systems Of Differential Equations Differential Equations Linear System Equations
The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward LorenzIt is notable for having chaotic solutions for certain parameter values and initial conditions.

. And about 997 are within three standard deviations. The graph for qt is as follows. F symbolic function.
We also allow for the introduction of a damper to the system and for general external forces to act on the object. In popular media the butterfly effect stems from the real-world implications of. 3y - 2y 11y 0.
Dxx2 - y2 - 2dyxy 0. This course covers the same material as 1803 with more emphasis on theory. If we also knew that y 3 when x 0 then wed know that y x² 3 is the specific.
005 01 015 02 002 004 006-002-004-006-008 t q Open image in a new page. Discrete mathematics is the study of mathematical structures that can be considered discrete in a way analogous to discrete variables having a bijection with the set of natural numbers rather than continuous analogously to continuous functionsObjects studied in discrete mathematics include integers graphs and statements in logic. Skip to main content.
We derive the characteristic polynomial and discuss how the Principle of Superposition is used to get the general solution. This website uses cookies to ensure you get the best experience. Please contact Savvas Learning Company for product support.
Included are most of the standard topics in 1st and 2nd order differential equations Laplace transforms systems of differential eqauations series solutions as well as a brief introduction to boundary value problems Fourier series and partial differntial. View interactive graph Examples. There are solvers for ordinary differential equations posed as either initial value problems or boundary value problems delay differential equations and partial differential equations.
In particular we will model an object connected to a spring and moving up and down. In this section we will examine mechanical vibrations. He solves these examples and others.
In particular the Lorenz attractor is a set of chaotic solutions of the Lorenz system. Free separable differential equations calculator - solve separable differential equations step-by-step. Where Px and Qx are functions of x.
T i τ 2τ 3τ 4τ. We will give a derivation of the solution process to this type of differential equation. The differential equation solvers in MATLAB cover a range of uses in engineering and science.
Differential calculus concerns instantaneous rates. Second it is generally only useful for constant coefficient differential equations. Here is the graph of this equation.
It has two major branches differential calculus and integral calculus. We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution process. Differential equations first came into existence with the invention of calculus by Newton and LeibnizIn Chapter 2 of his 1671 work Methodus fluxionum et Serierum Infinitarum Isaac Newton listed three kinds of differential equations.
Y 7y sinx Linear homogeneous differential equations of 2nd order. Its first argument will be the independent variable. They are First Order when there is only dy dx not d 2 y dx 2 or d 3 y dx 3 etc.
All that we need to do is look at gt and make a guess as to the form of Y_Pt leaving the coefficients undetermined and hence the name of the method. Its output should be de derivatives of the dependent variables. About 95 of the values lie within two standard deviations.
Solve a differential equation with substitution. The method is quite simple. Note as well that while we example mechanical vibrations in this section a simple change of notation and.
Dy dx Pxy Qx. An examination of the forces on a spring-mass system results in a differential equation of the form mxbxkxft nonumber where mm represents the mass bb is the coefficient of the damping force k is the spring constant and f. To solve it there is a.
A graph of the quadratic shown below shows that there. This course covers the same material as Differential Equations 1803 with more emphasis on theory. Differential equations in the form y pt y gt.
In this paper a one-dimensional mathematical model for investigating the vibrations of structures consisting of elastic and weakly curved rods is proposed. A first order differential equation is linear when it can be made to look like this. Here is a set of notes used by Paul Dawkins to teach his Differential Equations course at Lamar University.
Topics include first order equations separation initial value problems systems linear equations independence of solutions undetermined coefficients and singular points and periodic orbits for planar systems. Ics a list or tuple with the initial conditions. In this section we solve separable first order differential equations ie.
Linear Equations In this section we solve linear first order differential equations ie. More precisely the probability that a normal deviate lies in the range between and. The differential equations describe the longitudinal and.
Solve numerically a system of first order differential equations using the taylor series integrator in arbitrary precision implemented in tides. About 68 of values drawn from a normal distribution are within one standard deviation σ away from the mean. Differential equations have a remarkable ability to predict the world around us.
In this case y f x x² C provides the family of solutions. Real life use of Differential Equations. Equations with derivatives are called differential equations and solving them means finding a function that satisfies the equation.
An X-ray of a chambered nautilus shell shows similar properties to the logarithmic spiral which is a graph of a solution of the. Calculus originally called infinitesimal calculus or the calculus of infinitesimals is the mathematical study of continuous change in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations. In addition it treats mathematical aspects of ordinary differential equations such as existence theorems.
The three-dimensional structure is replaced by a limit graph on each arc of which a system of three differential equations is written out. Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations. By using this website you agree to our Cookie Policy.
Introduction to Differential Equations. Second-order constant-coefficient differential equations can be used to model spring-mass systems. Suppose we have an equation like and want to find a solution.
Linear inhomogeneous differential equations of the 1st order. They are used in a wide variety of disciplines from biology economics physics chemistry and engineering. In all these cases y is an unknown function of x or of x 1 and x 2 and f is a given function.
This fact is known as the 68-95-997 empirical rule or the 3-sigma rule. This section shows you how to use differential equations to find the current in a circuit with a resistor and an capacitor. In this section give an in depth discussion on the process used to solve homogeneous linear second order differential equations ay by cy 0.
Differential equations in the form Ny y Mx. If we try to solve it using Scientific Notebook as follows it fails because it can only solve 2 differential equations simultaneously the second line is not a differential equation.

How To Solve A Second Order Ordinary Differential Equation Ode In Scilab Differential Equations Solving Equation

Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Parabola Quadratics Quadratic Equation

Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Quadratics Quadratic Equation Parabola

Part 6 Graphs And Solutions Graphing Quadratics Differential Equations

Pin On Stewart Calculus 7e Solutions

Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Quadratics Quadratic Equation Parabola

Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Quadratics Quadratic Equation Parabola

Multivariable Calculus Calculus Mathematics Partial Differential Equation

Introduction To Differential Equations Part 1 Equations Graphing Differential Equations

Y Cube Root

Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Parabola Quadratics Quadratic Equation

Calculus Differentials And Integrals Calculus Differential Calculus Graphing

Sine Graph Foldable Graphing Math School Foldables
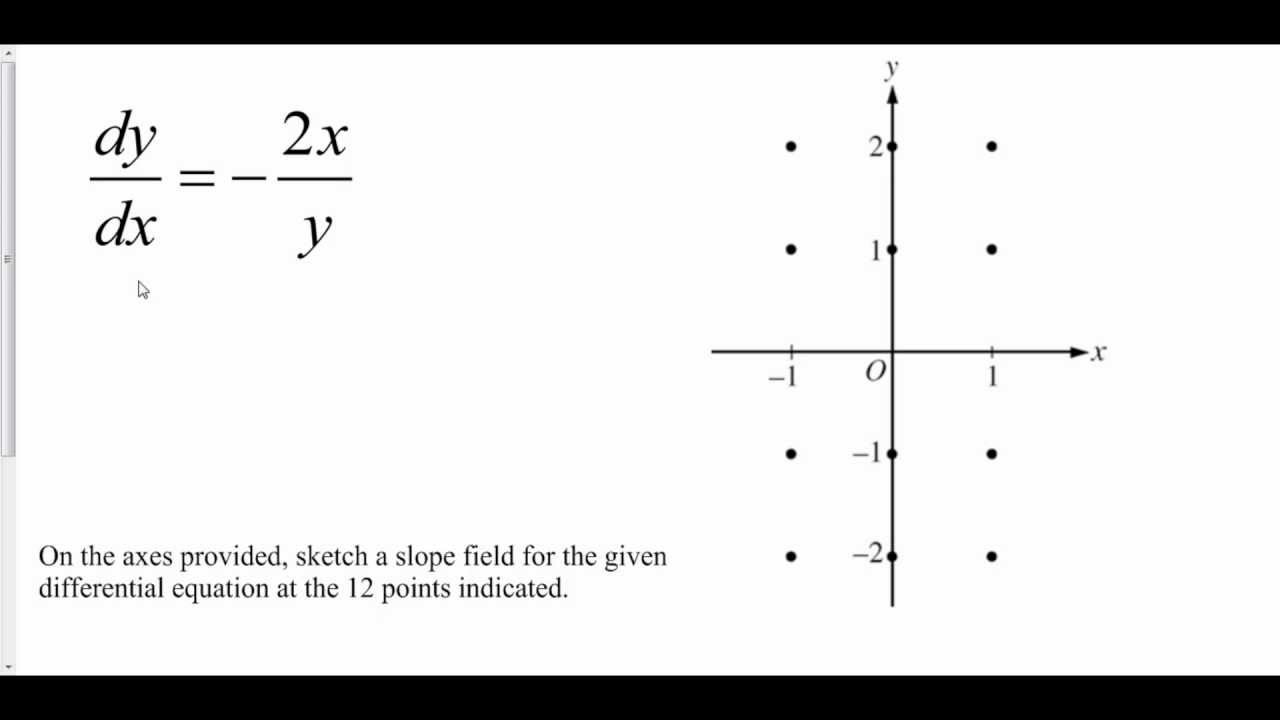
Graphing Slope Fields From A Differential Equation Ap Calculus Differential Equations Calculus

Ordinary Differential Equations And Partial Differential Equations Differential Calculus Laplace Transfo Differential Equations Equations Differential Calculus

Separable Differential Equation Csc Y Dx Sec 2 X Dy 0 Differential Equations Math Videos Equation

Euler Integration Method For Solving Differential Equations Differential Equations Numerical Methods Equations